2D Shallow water equations

Simulates the 2D shallow water equations with conservative variables. The problem is described with the following system of PDE

$$\begin{array}{r}\begin{array}{c}\frac{\partial h}{\partial t}+\frac{\partial hu}{\partial x}+\frac{\partial hv}{\partial y}=0\\ \frac{\partial hu}{\partial t}+\frac{\partial }{\partial x}(h{u}^2+\frac{1}{2}g{h}^2)+\frac{\partial huv}{\partial y}=-\mu v\\ \frac{\partial hv}{\partial t}+\frac{\partial huv}{\partial x}+\frac{\partial }{\partial y}(h{v}^2+\frac{1}{2}g{h}^2)=\mu u\end{array}\end{array}$$

for fluid column height $h$, gravity $g$ and 2D vector $(u,v)$ of the fluid’s horizontal flow velocity averaged across the vertical column.

• Domain is $[-5,5{]}^2$ with slip-wall BCs

• Initial conditions:

  • $h=1+\alpha \exp (-(x-1{)}^2-(y-1{)}^2)$

  • $u=0$

  • $v=0$

• Default settings:

  • $\alpha =1/8$ (initial pulse magnitude)

  • $g=9.8$ (gravity parameter)

  • $\mu =-3.0$ (Coriolis parameter)

• $g,\mu ,\alpha$ can be provided to the problem constructor (more below)

Mesh

python3 pressio-demoapps/meshing_scripts/create_full_mesh_for.py \
        --problem swe2dSlipWall_s<stencilSize> -n Nx Ny --outDir ...

where

• Nx, Ny is the number of cells you want along $x$ and $y$ respectively

• <stencilSize> = 3 or 5 or 7: defines the neighboring connectivity of each cell

• <destination-path> is where you want the mesh files to be generated. The script creates the directory if it does not exist.

Important

When you set the <stencilSize>, keep in mind the following constraints (more on this below):

• InviscidFluxReconstruction::FirstOrder requires <stencilSize> >= 3

• InviscidFluxReconstruction::Weno3 requires <stencilSize> >= 5

• InviscidFluxReconstruction::Weno5 requires <stencilSize> >= 7

C++ synopsis

#include "pressiodemoapps/swe2d.hpp"

int main(){
  namespace pda = pressiodemoapps;

  const auto meshObj = pda::load_cellcentered_uniform_mesh_eigen("path-to-mesh");

  const auto scheme = pda::InviscidFluxReconstruction::FirstOder; //or Weno3, Weno5

  // A. constructor for problem using default values
  {
    const auto probId = pda::Swe2d::SlipWall;
    auto problem = pda::create_problem_eigen(meshObj, probId, scheme);
  }

  // B. constructor for problem specifying all coefficients
  {
    using scalar_type   = typename decltype(meshObj)::scalar_t;
    const scalar_type gravity  = /* some value */;
    const scalar_type coriolis = /* some value */;
    const scalar_type alpha    = /* some value */;

    auto problem = pda::create_slip_wall_swe_2d_problem_eigen(meshObj, scheme,
                                                              gravity, coriolis, alpha);
  }
}

Python synopsis

import pressiodemoapps as pda

meshObj = pda.load_cellcentered_uniform_mesh_eigen("path-to-mesh")

probId  = pda.Swe2d.SlipWall;
scheme  = pda.InviscidFluxReconstruction.FirstOrder # or Weno3, Weno5

# A. constructor for problem using default values
problem = pda.create_problem(meshObj, probId, scheme)

# B. constructor for problem specifying all coefficients
gravity  = # some value
coriolis = # some value
alpha    = # some value
problem = pda.create_slip_wall_swe_2d_problem(meshObj, scheme, gravity, coriolis, alpha)

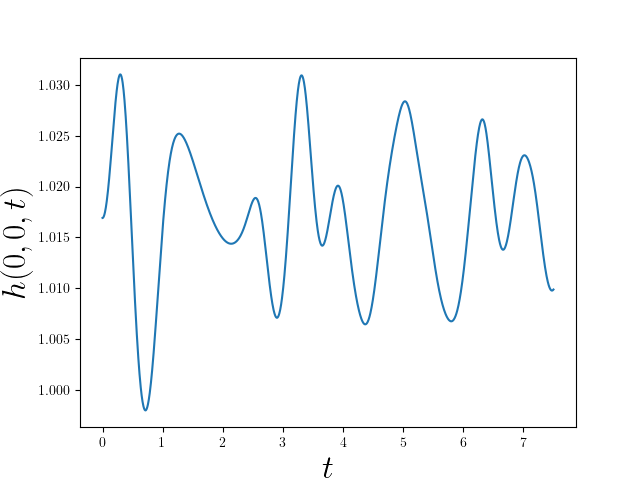
Sample Plot

Representative plot of the height $h(t)$ as a function of time at $x=y=0$ using default physical parameters, a 65x65 mesh with Weno5 and RK4 time integration: