2D Euler Kelvin-Helmholtz#

This problem solves the 2D conservative Euler equations

\[\begin{split}\frac{\partial }{\partial t} \begin{bmatrix}\rho \\ \rho u_x \\ \rho u_y\\ \rho E \end{bmatrix} + \frac{\partial }{\partial x} \begin{bmatrix}\rho u_x \\ \rho u_x^2 +p \\ \rho u_x u_y \\ (E+p)u_x \end{bmatrix} \frac{\partial }{\partial y} \begin{bmatrix}\rho u_y \\ \rho u_x u_y \\ \rho u_y^2 +p \\ (E+p)u_y \end{bmatrix}= 0\end{split}\]

where the pressure \(p\) is related to the conserved quantities through the equation of the state

\[p=(\gamma -1)(\rho E-\frac{1}{2}\rho (u_x^2 + u_y^2)).\]

  • Domain is \(\Omega = \Omega_1 \cup \Omega_2 = [-5,5]^2\) with periodic BC where:

    • \(\Omega_1 = [-5,5] \times [-2 + \cos( 0.8 \pi x) , 2 + \cos(0.8 \pi x)]\)

    • \(\Omega_2\): Rest of the domain

  • Initial conditions in primitive variables:

    • in \(\Omega_1\): \(\rho = 2, u = 0.5, v = 0, p = 2.5\)

    • in \(\Omega_2\): \(\rho = 1, u = -0.5, v = 0, p = 2.5\)

    • This IC is used to create the corresponding initial conditions in conservative variables.

  • By default, \(\gamma = 1.4\)

  • Time integration performed for 2.5 flow through units, \(t \in (0, 50)\)

  • Mach number in \(\Omega_1\) : \(M_{\infty} = 0.377964\)

  • Mach number in \(\Omega_2\) : \(M_{\infty} = 0.267261\)

  • This problem is often unstable for a standard Galerkin ROM

Mesh#

python3 pressio-demoapps/meshing_scripts/create_full_mesh_for.py \
        --problem euler2dKelvinHelmholtz_s<stencilSize> -n Nx Ny --outDir <destination-path>

where

  • Nx, Ny is the number of cells you want along \(x\) and \(y\) respectively

  • <stencilSize> = 3 or 5 or 7: defines the neighboring connectivity of each cell

  • <destination-path> is where you want the mesh files to be generated. The script creates the directory if it does not exist.

Important

When you set the <stencilSize>, keep in mind the following constraints (more on this below):

  • InviscidFluxReconstruction::FirstOrder requires <stencilSize> >= 3

  • InviscidFluxReconstruction::Weno3 requires <stencilSize> >= 5

  • InviscidFluxReconstruction::Weno5 requires <stencilSize> >= 7

C++ synopsis#

#include "pressiodemoapps/euler2d.hpp"

int main(){
  namespace pda     = pressiodemoapps;

  const auto meshObj = pda::load_cellcentered_uniform_mesh_eigen("path-to-mesh");

  const auto probId = pda::Euler2d::KelvinHelmholtz;
  const auto scheme = pda::InviscidFluxReconstruction::FirstOrder; //or Weno3, Weno5
  auto problem      = pda::create_problem_eigen(meshObj, probId, scheme);
  auto state      = problem.initialCondition();
}

Python synopsis#

import pressiodemoapps as pda

meshObj = pda.load_cellcentered_uniform_mesh("path-to-mesh")

probId  = pda.Euler2d.KelvinHelmholtz
scheme  = pda.InviscidFluxReconstruction.FirstOrder # or Weno3, Weno5
problem = pda.create_problem(meshObj, probId, scheme)
state   = problem.initialCondition()

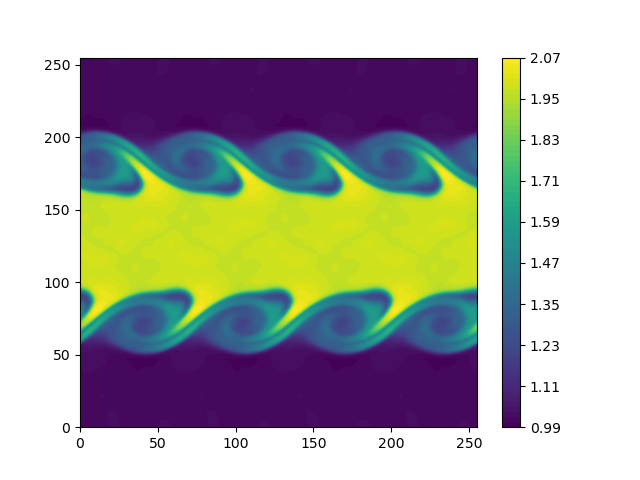
Sample Plot#

Representative density field at selected time \(t=50\) using a 256x256 mesh with Weno5 and RK4 time integration:

Alternative text