2D Burgers (Periodic BCs)

This problem solves the following 2D nonlinear viscous Burgers equations

\[ \begin{align}\begin{aligned}\frac{\partial u}{\partial t} + \frac{1}{2} \frac{\partial u^2}{\partial x} + \frac{1}{2} \frac{\partial u v}{\partial y} &= D \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right)\\\frac{\partial v}{\partial t} + \frac{1}{2} \frac{\partial u v}{\partial x} + \frac{1}{2} \frac{\partial v^2}{\partial y} &= D \left( \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} \right)\end{aligned}\end{align} \]

• Domain is \([-1,1]^2\) with periodic BC

• Initial conditions are: \(u = v = \alpha \exp( - \frac{(x-x_0)^2+(y-y_0)^2}{\delta} )\)

• Default settings: \(\alpha = 0.5\), \(\delta = 0.15\), \(x_0=0, y_0=-0.2\), \(D = 0.00001\)

Mesh

python3 pressio-demoapps/meshing_scripts/create_full_mesh_for.py \
        --problem burgers2d_periodic_s<stencilSize> -n Nx Ny --outDir <destination-path>

where

• Nx, Ny is the number of cells you want along \(x\) and \(y\) respectively

• <stencilSize> = 3 or 5 or 7: defines the neighboring connectivity of each cell

• <destination-path> is where you want the mesh files to be generated. The script creates the directory if it does not exist.

Important

When you set the <stencilSize>, keep in mind the following constraints (more on this below):

• InviscidFluxReconstruction::FirstOrder requires <stencilSize> >= 3

• InviscidFluxReconstruction::Weno3 requires <stencilSize> >= 5

• InviscidFluxReconstruction::Weno5 requires <stencilSize> >= 7

C++ synopsis

#include "pressiodemoapps/advection_diffusion2d.hpp"

int main(){
  namespace pda = pressiodemoapps;

  const auto meshObj = pda::load_cellcentered_uniform_mesh_eigen("path-to-mesh");

  const auto inviscidScheme = pda::InviscidFluxReconstruction::FirstOrder; // or Weno3, Weno5
  const auto viscousScheme  = pda::ViscousFluxReconstruction::FirstOrder;  // must be FirstOrder

  // A. constructor for problem using default values
  {
    const auto probId = pda::AdvectionDiffusion2d::BurgersPeriodic;
    auto problem = pda::create_problem_eigen(meshObj, probId, inviscidScheme, viscousScheme);
  }

  // B. setting custom coefficients
  {
    using scalar_type = typename decltype(meshObj)::scalar_t;
    const auto alpha  = /* something */;
    const auto delta  = /* something */;
    const auto D      = /* something */;
    const auto x0     = /* something */;
    const auto y0     = /* something */;
    auto problem = pda::create_periodic_burgers_2d_problem_eigen(meshObj, inviscidScheme,
                                                                 viscousScheme, alpha,
                                                                 delta, D, x0, y0)
  }
}

Python synopsis

import pressiodemoapps as pda

meshObj = pda.load_cellcentered_uniform_mesh("path-to-mesh")

inviscidScheme = pda.InviscidFluxReconstruction.FirstOrder; # or Weno3, Weno5
viscousScheme  = pda.ViscousFluxReconstruction.FirstOrder;  # must be FirstOrder

# A. constructor for problem using default values
probId  = pda.AdvectionDiffusion2d.BurgersPeriodic
problem = pda.create_problem(meshObj, probId, inviscidScheme, viscousScheme)

# B. setting custom coefficients
alpha  = # something
delta  = # something
D      = # something
x0     = # something
y0     = # something
problem = pda.create_periodic_burgers_2d_problem(meshObj, inviscidScheme,
                                                 viscousScheme, alpha,
                                                 delta, D, x0, y0)

Sample Plot

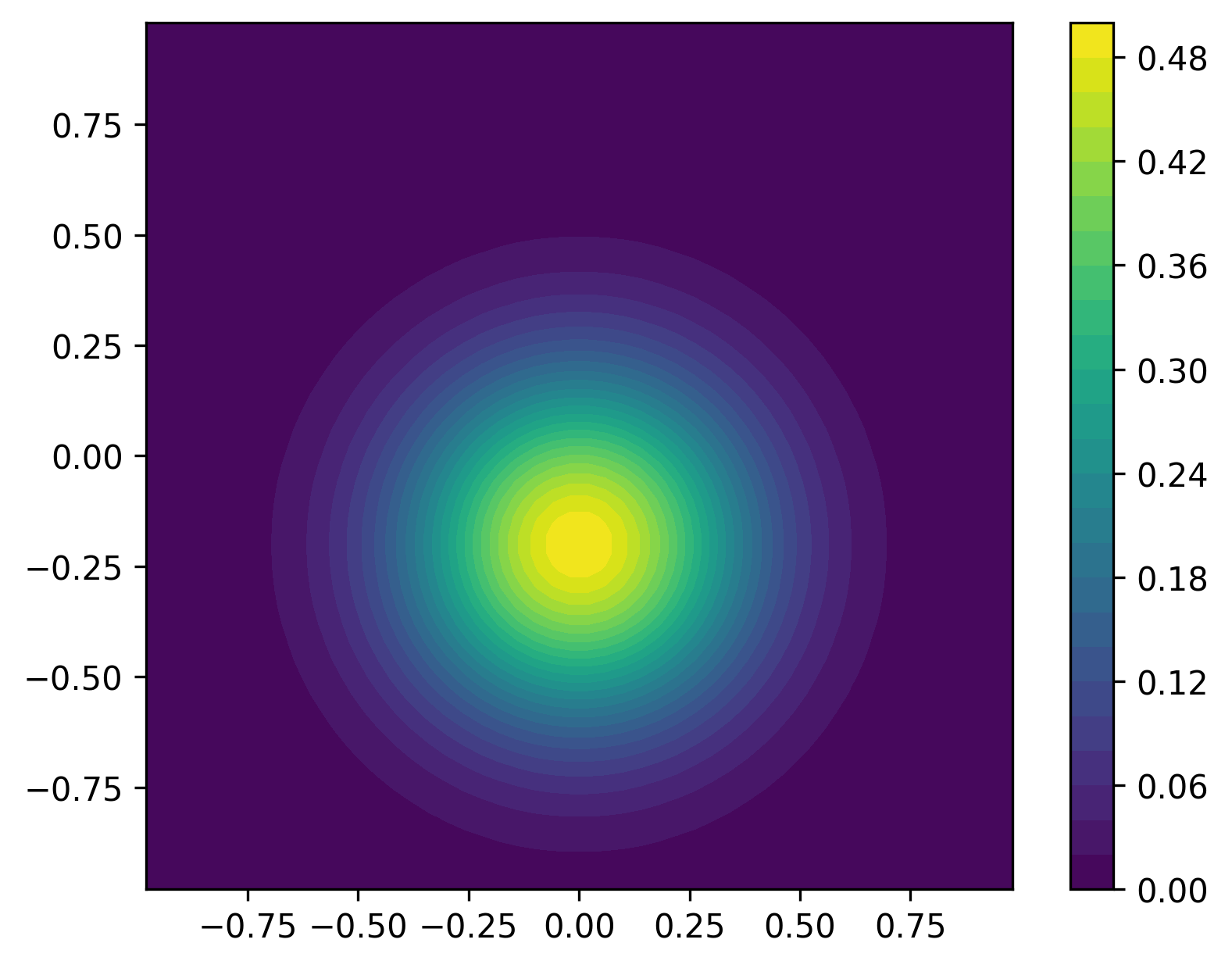
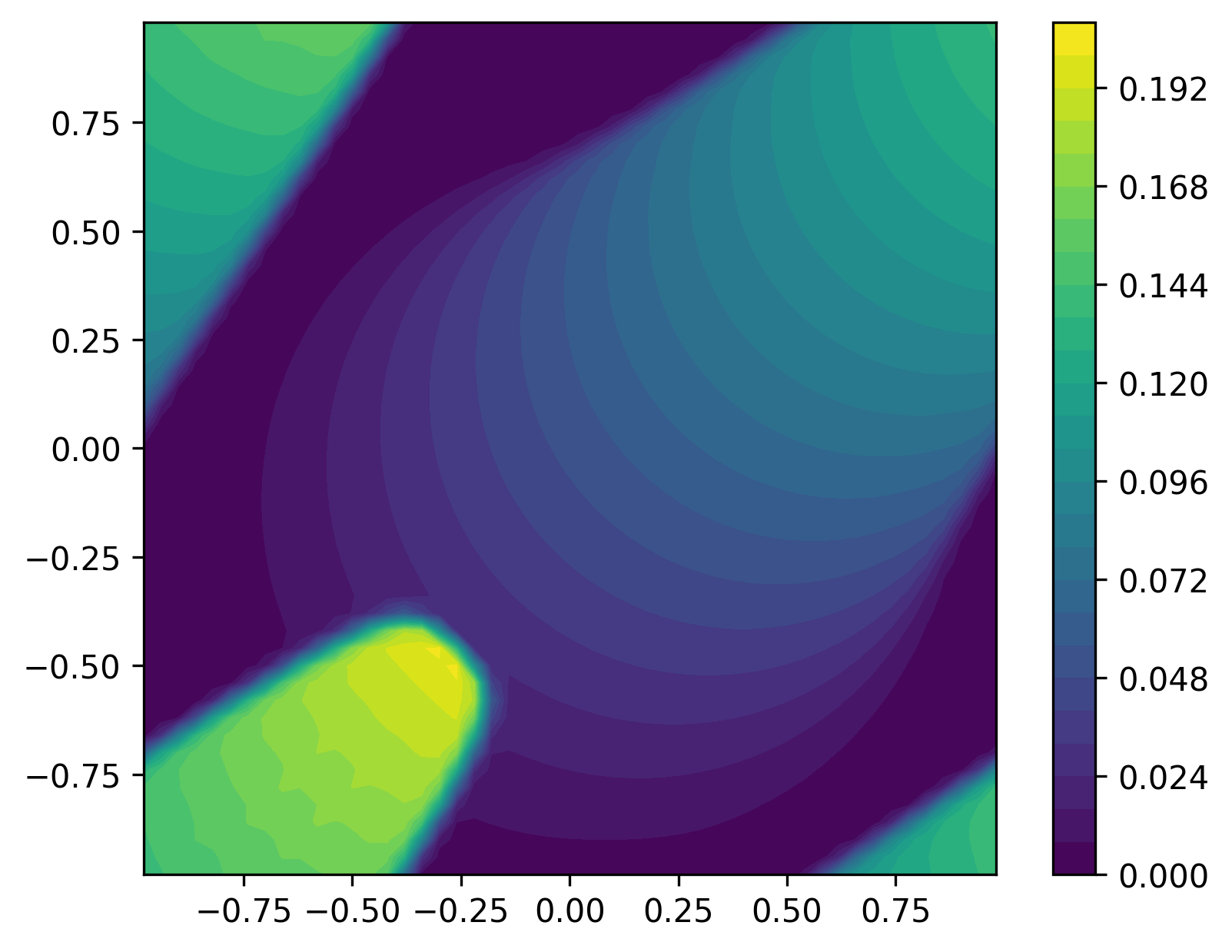
Representative plot of u at \(t=0\) (left) and \(t=10.\), using a 50x50 mesh with Weno5 and RK4 time integration with \(dt = 0.005\), and the default settings for the parameters:

Notes:

Important

Note that we currently support only first order viscous flux reconstruction, which leads to a second-order scheme.