1D adv-diff: POD Galerkin with collocation masking

Overview

We cover these steps:

1. generate of snapshots using the full-order model (FOM)
2. compute the POD basis
3. create the masking operator
4. execute the ROM: here we leverage the GALERKIN ROM to demonstrate a reproductive test, i.e., we run the ROM using the same physical coefficients, b.c., etc.

The key item introduced here is the "masking" operator. In simple words, masking allows us to mimic the effect of the hyper-reduction without changing the application code. Hyper-reduction is a fundamental part of ROMs needed to approximate the FOM operators, thus contributing significantly to the computational cost savings. However, the main difficulty of hyper-reduction is that it generally is quite intrusive to be done properly.

To briefly explain what hyper-reduction, let's look at the most basic form of hyper-reduction, namely "collocation". Consider the following system of N ODEs:

A collocation-based hyper-reduction involves approximating the right-hand side by computing only at a subset of grid points. Obviously, the way we compute the locations to select is critical and there are several techniques available to do so. Here, we show a simple example just for demonstration purposes of performing collocation with randomly selected points

FOM Equations

The governing equations for this problem are:

where , the field is , the advection velocity is fixed at , the spatial coordinate is and the domain is . We use homogeneous BC. Note that a class approximating the FOM operators via finite-differences is implemented here.

Main function

The main function of the demo is the following:

logger.initialize(logger.logto.terminal)
logger.setVerbosity([logger.loglevel.info])

# total number of grid points
meshSize = 200

# create fom object
fomObj = AdvDiff1d(nGrid=meshSize, adv_coef=1.0)

# the final time to integrate to
finalTime = .05

#--- 1. FOM ---#
fomTimeStepSize  = 1e-5
fomNumberOfSteps = int(finalTime/fomTimeStepSize)
sampleEvery      = 100
[fomFinalState, snapshots] = doFom(fomObj, fomTimeStepSize, fomNumberOfSteps, sampleEvery)

#--- 2. POD ---#
modes = computePodModes(snapshots)

#--- 3. MASKED GALERKIN ROM ---#
romSize = 10  # number of modes to use
romTimeStepSize  = 1e-4
romNumberOfSteps = int(finalTime/romTimeStepSize)

# a masked galerkin is supposed to make it easier to emulate the
# effect of hyper-reduction. To create a mask ROM problem,
# we need to select and provide to pressio a set of indices
# identifying a subset of the grid points in the full mesh.
# This is a simple way to mimic hyper-reduction
# without changing the FOM problem. In fact, the fom still
# computes the full operators but we have an additional step
# to "mask" the operators to compute the sample mesh version.
# In this test, the meshSize = 200. Our sample mesh includes
# the two end points since those contain the boundary conditions,
# and 150 randomly selected grid points inside the domain.
# So effectively we use 25% less of the full mesh.
random.seed(312367)
sampleMeshSize = 150
sampleMeshIndices = random.sample(range(1, 199), sampleMeshSize)
sampleMeshIndices = np.append(sampleMeshIndices, [0, 199])

# run the masked galerkin problem
approximatedState = runMaskedGalerkin(fomObj, romTimeStepSize,
                                      romNumberOfSteps, modes[:,:romSize],
                                      sampleMeshIndices)

# compute l2-error between fom and approximate state
fomNorm = linalg.norm(fomFinalState)
err = linalg.norm(fomFinalState-approximatedState)
print("Final state relative l2 error: {}".format(err/fomNorm))

logger.finalize()

def doFom(fom, dt, nsteps, saveFreq):
  u = fom.u0.copy()
  U = [u]
  f = fom.createVelocity()
  for i in range(1,nsteps+1):
    # query rhs of discretized system
    fom.velocity(u, i*dt, f)
    # simple Euler forward
    u = u + dt*f
    if i % saveFreq == 0:
      U.append(u)
  Usolns = np.array(U)
  return [u, Usolns.T]

def computePodModes(snapshots):
  print("SVD on matrix: ", snapshots.shape)
  U,S,VT = np.linalg.svd(snapshots)
  return U

# effect of hyper-reduction. To create a mask ROM problem,
# we need to select and provide to pressio a set of indices
# identifying a subset of the grid points in the full mesh.
# This is a simple way to mimic hyper-reduction
# without changing the FOM problem. In fact, the fom still
# computes the full operators but we have an additional step
# to "mask" the operators to compute the sample mesh version.
# In this test, the meshSize = 200. Our sample mesh includes
# the two end points since those contain the boundary conditions,
# and 150 randomly selected grid points inside the domain.
# So effectively we use 25% less of the full mesh.
random.seed(312367)
sampleMeshSize = 150
sampleMeshIndices = random.sample(range(1, 199), sampleMeshSize)
sampleMeshIndices = np.append(sampleMeshIndices, [0, 199])

class MyMasker:
  def __init__(self, indices):
    self.rows_ = indices
    self.sampleMeshSize_ = len(indices)

  def createApplyMaskResult(self, operand):
    return np.zeros(self.sampleMeshSize_)

  def __call__(self, operand, time, result):
    result[:] = np.take(operand, self.rows_)

def runMaskedGalerkin(fomObj, dt, nsteps, modes, sampleMeshIndices):
  # find out number of modes wanted
  romSize = modes.shape[1]

  # fom reference state: here it is zero
  fomReferenceState = np.zeros(fomObj.nGrid)

  # create ROM state by projecting the fom initial condition
  fomInitialState = fomObj.u0.copy()
  romState = np.dot(modes.T, fomInitialState)

  '''
  creating a masked Galerkin problem involves these steps:
  (1) creating the decoder on the FULL mesh
  (2) create a "projector operator" by filtering the rows
      of the POD modes only on the sample mesh (aka mask) indices.
      The projector is responsible to project the FOM velocity.
      Note that one can use other matrices for the projector
      but that will be shown in other demos.
  (3) create a masker object responsible to mask the FOM operators.
  (4) create the masked Galerkin problem
  '''

  # 1. create a linear decoder
  linearDecoder = rom.Decoder(modes)

  # 2. create the projector
  # here, simply use "collocation" with the POD modes filtered on the "sample mesh"
  modesOnSampleMesh = np.take(modes, sampleMeshIndices, axis=0)
  projector = MyProjector(modesOnSampleMesh)

  # 3. create the masker object
  masker = MyMasker(sampleMeshIndices)

  # 4. create the masked galerkin problem with Euler forward
  scheme = ode.stepscheme.ForwardEuler
  problem = rom.galerkin.MaskedExplicitProblem(scheme, fomObj, linearDecoder, \
                                               romState, fomReferenceState, \
                                               projector, masker)

  # solve problem
  ode.advance_n_steps(problem, romState, 0., dt, nsteps)

  # after we are done, use the reconstructor object to reconstruct the fom state
  # NOTE: even though the Galerkin problem was run on the "masked mesh points",
  # this reconstruction uses the POD modes on the full mesh stored in the decoder
  # so we can effectively obtain an approximation of the full solution
  fomRecon = problem.fomStateReconstructor()
  return fomRecon(romState)

Results

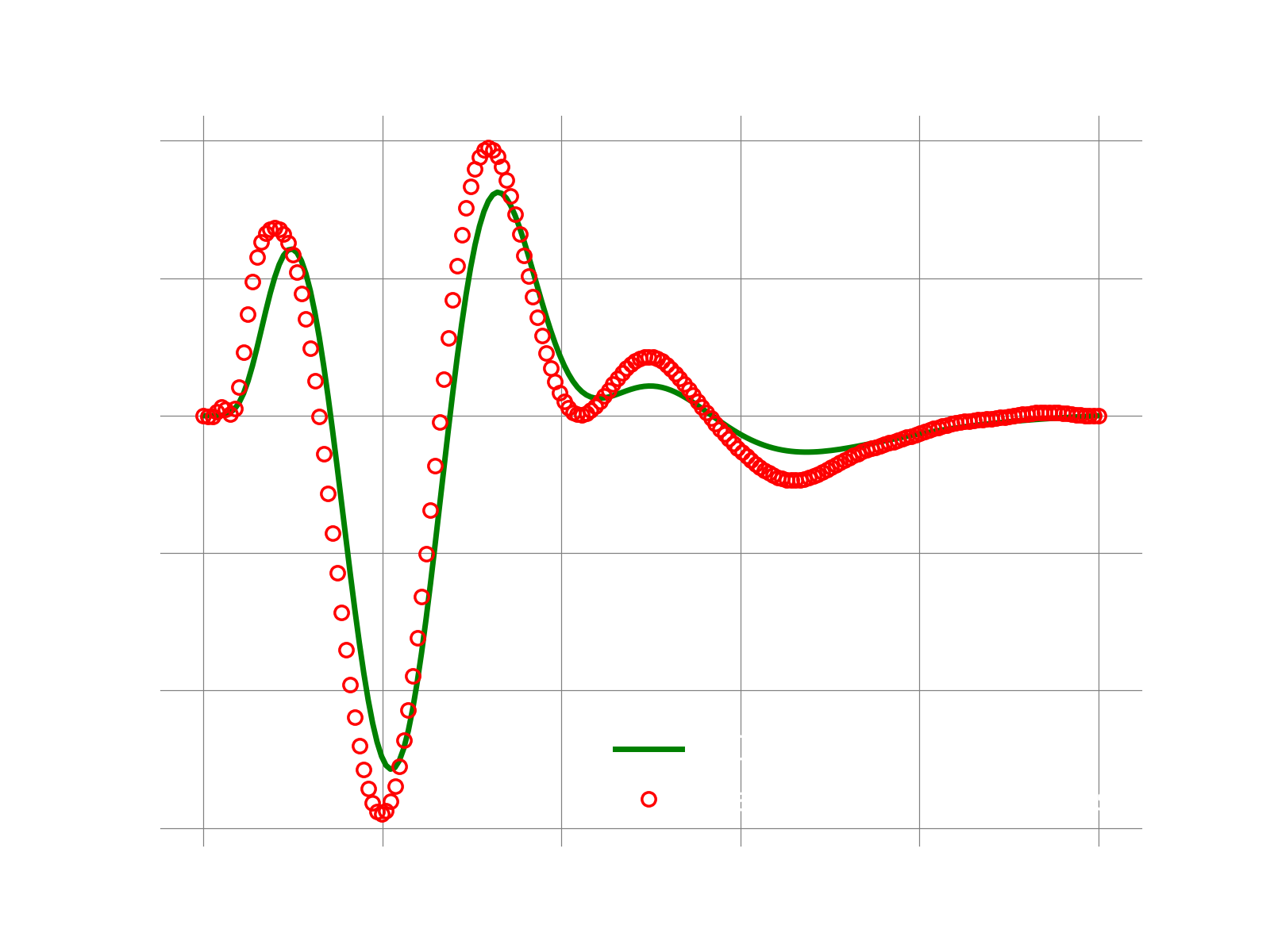
If everything works fine, the following plot shows the result. We see that for this toy example, the full solution is recovered very well with Galerkin with just a few POD modes.