1D adv-diff: LSPG with POD modes
Overview
We cover these three typical steps needed for a ROM:
- generate of snapshots using the full-order model (FOM)
- compute the basis: here we demonstrate the use of POD modes
- execute the ROM: here we leverage the LSPG ROM to demonstrate a reproductive test, i.e., we run the ROM using the same physical coefficients, b.c., etc. A predictive run is demonstrated in a different tutorial.
The governing equations for this problem are the same as those in here,
Main function
The main function of the demo is the following:
logger.initialize(logger.logto.terminal) logger.setVerbosity([logger.loglevel.info]) # create fom object fomObj = AdvDiff1d(nGrid=120, adv_coef=2.0) # the final time to integrate to finalTime = .05 #--- 1. FOM ---# fomTimeStepSize = 1e-5 fomNumberOfSteps = int(finalTime/fomTimeStepSize) sampleEvery = 200 [fomFinalState, snapshots] = doFom(fomObj, fomTimeStepSize, fomNumberOfSteps, sampleEvery) #--- 2. POD ---# modes = computePodModes(snapshots) #--- 3. LSPG ROM ---# romSize = 4 romTimeStepSize = 3e-4 romNumberOfSteps = int(finalTime/romTimeStepSize) # we pass only romSize modes approximatedState = runLspg(fomObj, romTimeStepSize, romNumberOfSteps, modes[:,:romSize]) # compute l2-error between fom and approximate state fomNorm = linalg.norm(fomFinalState) err = linalg.norm(fomFinalState-approximatedState) print("Final state relative l2 error: {}".format(err/fomNorm)) logger.finalize()
1. Run FOM and collect snapshots
def doFom(fom, dt, nsteps, saveFreq): u = fom.u0.copy() U = [u] f = fom.createVelocity() for i in range(1,nsteps+1): # query rhs of discretized system fom.velocity(u, i*dt, f) # simple Euler forward u = u + dt*f if i % saveFreq == 0: U.append(u) Usolns = np.array(U) return [u, Usolns.T]
2. Compute POD modes
def computePodModes(snapshots): print("SVD on matrix: ", snapshots.shape) U,S,VT = np.linalg.svd(snapshots) return U
3. Construct and run ROM
def runLspg(fomObj, dt, nsteps, modes): # this is an auxiliary class that can be passed to solve # LSPG to monitor the rom state. class RomStateObserver: def __call__(self, timeStep, time, state): pass # this linear solver is used at each gauss-newton iteration class MyLinSolver: def solve(self, A,b,x): lumat, piv, info = linalg.lapack.dgetrf(A, overwrite_a=True) x[:], info = linalg.lapack.dgetrs(lumat, piv, b, 0, 0) #---------------------------------------- # find out number of modes wanted romSize = modes.shape[1] # create a linear decoder, passing only the desired number of modes # this will make a deep copy of the modes linearDecoder = rom.Decoder(modes) # fom reference state: here it is zero fomReferenceState = np.zeros(fomObj.nGrid) # create ROM state by projecting the fom initial condition fomInitialState = fomObj.u0.copy() romState = np.dot(modes.T, fomInitialState) # create LSPG problem scheme = ode.stepscheme.BDF1 problem = rom.lspg.unsteady.DefaultProblem(scheme, fomObj, linearDecoder, romState, fomReferenceState) # create the Gauss-Newton solver nonLinSolver = solvers.create_gauss_newton(problem, romState, MyLinSolver()) # set tolerance and convergence criteria nlsTol, nlsMaxIt = 1e-6, 5 nonLinSolver.setMaxIterations(nlsMaxIt) nonLinSolver.setStoppingCriterion(solvers.stop.WhenCorrectionAbsoluteNormBelowTolerance) # create object to monitor the romState at every iteration myObs = RomStateObserver() # solve problem ode.advance_n_steps_and_observe(problem, romState, 0., dt, nsteps, myObs, nonLinSolver) # after we are done, use the reconstructor object to reconstruct the fom state # get the reconstructor object: this allows to map romState to fomState fomRecon = problem.fomStateReconstructor() return fomRecon(romState)
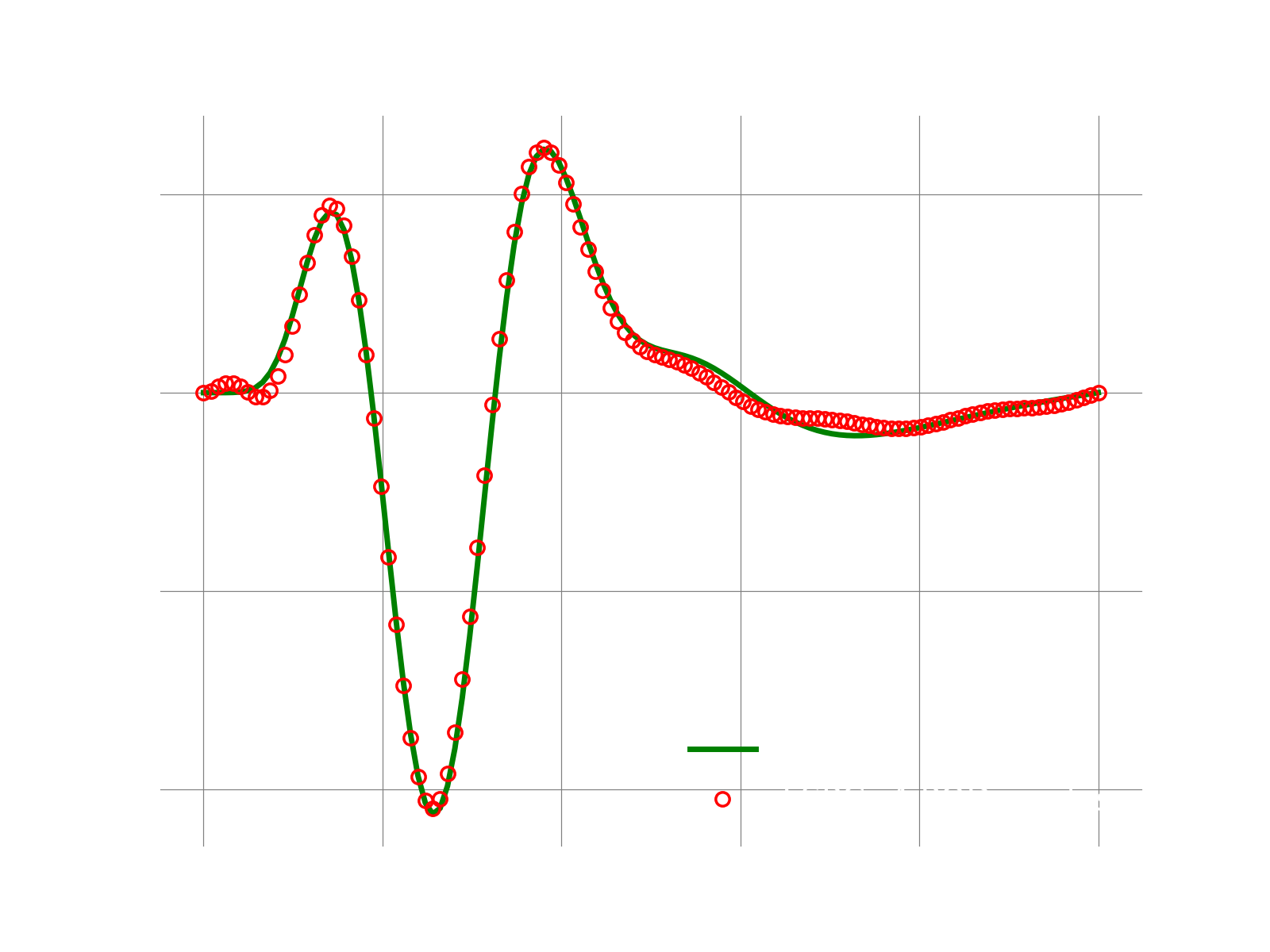
Results
If everything works fine, the following plot shows the result.