rom: LSPG: unsteady hyper-reduced problem

API, Parameters and Requirements

problem = lspg.unsteady.HypredProblem(scheme, fom_adapter, decoder, \
                                      rom_state, fom_ref_state, \
                                      sampleToStencilIndexing)

problem = lspg.unsteady.PrecHypredProblem(scheme, fom_adapter, decoder, \
                                          rom_state, fom_ref_state, \
                                          sampleToStencilIndexing, preconditioner)

• scheme:
  • value from the ode.stepscheme enum setting the desired stepping scheme
  • requires an implicit value
• fom_adapter:
  • instance of your adapter class specifying the FOM problem.
    
  • must be admissible to unsteady LSPG, see API list
• decoder:
  • decoder object
  • must satify the requirements listed here
• rom_state:
  • currently, must be a rank-1 numpy.array
• fom_ref_state:
  • your FOM reference state that is used when reconstructing the FOM state
  • must be a rank-1 numpy.array
• stencilToSampleIndexing:
  • an object that knows the mapping from sample to stancil operators
  • can be constructed as:
    mapper = rom.lspg.unsteady.StencilToSampleIndexing(list_of_ints)  
  • see section below for more details
• preconditioner:
  • functor needed to precondition the ROM operators

  • must be a functor with a specific API:

    class Prec:
      def __call__(self, fom_state, time, operand):
        # given the current FOM state,
        # apply your preconditioner to the operand.
        # Ensure that you overwrite the data in the operand.
        # As an example, a trivial preconditioner that does nothing:
        # operand[:] *= 1.

    
    

Stencil to sample indexing

When working with a hyper-reduced problem, pressio4py has to manipulate objects that have different sizes/distributions. For such problem, in fact, some operators are naturally defined on the what we refer to as "sample mesh" while some are defined on what we call the "stencil mesh".

As explained here, recall that:

1. sample mesh: a disjoint collection of elements where the velocity (or residual) operator is computed.
2. stencil mesh: the set of all nodes or elements needed to compute the velocity or residual on the sample mesh.
3. Typically, the sample mesh is a subset of the stencil mesh.

Explain it to me better!

Suppose that your FOM problem involves a 2D problem and that your FOM numerical method needs at every cell information from the nearest neighbors. For the sake of explanation, it does not matter what problem we are solving, only what we just said. Now, suppose that you want to try hyper-reduced LSPG on it. You come up with a sample and stencil mesh for your problem (read this page for some information about how to select sample mesh cells), and let's say it looks like this:

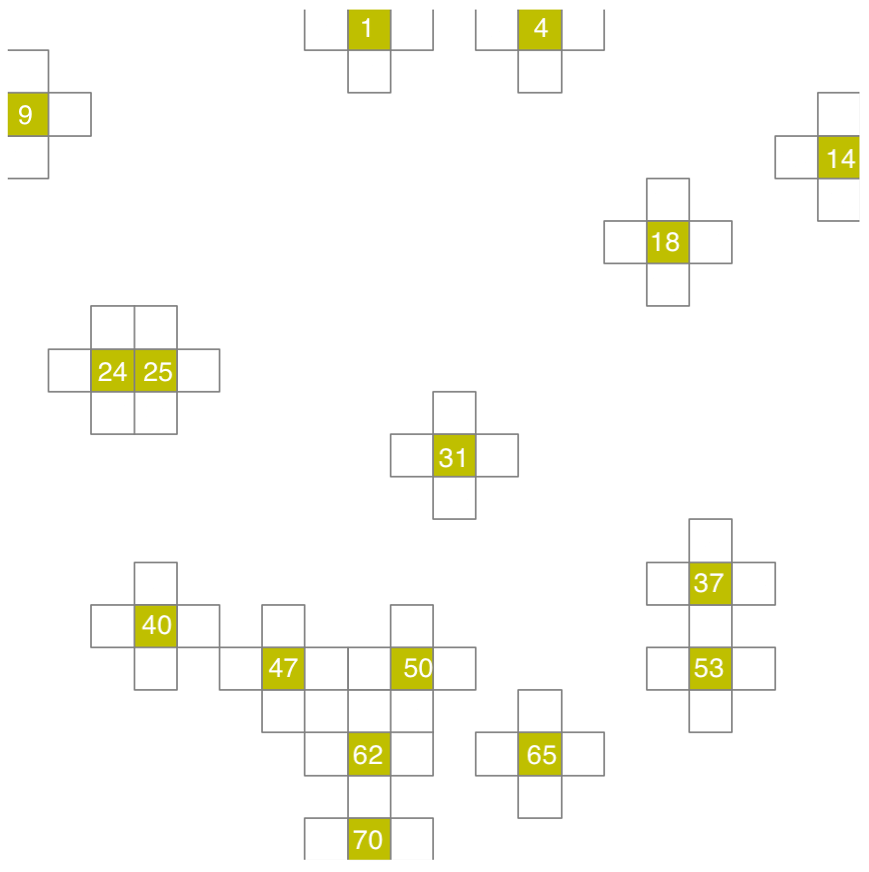
The stencil mesh is the set of all cells shown, while the sample mesh is the subset color-coded yellow. We have added an arbitrary enumeration scheme to uniquely assign a global index to each cell. The enumeration order does not matter, this is just for demonstration purposes. You have an adapter class for your problem that is able to compute the FOM right-hand-side on the yellow cells, for a given FOM state on the stencil mesh.

For this example, you then would do this:

# ...
mylist = [1,4,9,14,18,24,25,31,37,40,47,50,53,62,65,70]
indexing = rom.lspg.unsteady.StencilToSampleIndexing(mylist)
scheme = ode.stepscheme.BDF1
lspgProblem = rom.lspg.unsteady.HypredProblem(..., indexing)
# ...