POD vector space tutorial#

In this tutorial you will learn:

  • How to construct a vector space using proper orthogonal decomposition

  • How to use a truncater

#First, let's import the relavant modules:
import romtools
import numpy as np
from matplotlib import pyplot as plt
from romtools import vector_space

#Now, we will load in snapshots from a FOM. Here, we use pre-computed snapshots of the 1D Euler equations obtained using pressio-demo-apps
snapshots = np.load('snapshots.npz')['snapshots']

## The snapshots are in tensor form:
n_vars, nx, nt = snapshots.shape
## Note that romtools works with tensor forms (https://pressio.github.io/rom-tools-and-workflows/romtools/vector_space.html)

#Now, let's make a basis using POD that uses the first vector as an affine offset
#First, let's create a "shifter" that is responsible for shifting snapshots
#(https://pressio.github.io/rom-tools-and-workflows/romtools/vector_space/utils/shifter.html)
my_shifter = vector_space.utils.create_firstvec_shifter(snapshots)

#Now, let's create a truncater that controls for how we want to truncate our basis.
#(https://pressio.github.io/rom-tools-and-workflows/romtools/vector_space/utils/truncater.html)
#Let's use an energy-based criterion
my_truncater = vector_space.utils.EnergyBasedTruncater(0.999)

#Now, let's construct an affine vector space using POD with our shifter and truncater
#Note we don't use the first snapshot in the vector space since this is the affine offset
my_affine_vector_space = vector_space.VectorSpaceFromPOD(snapshots[...,1::],truncater=my_truncater,shifter=my_shifter)

##It's important to note that we do not do a deep copy of the snapshot matrix for performance reasons.
##Once you pass us the snapshot tensor, we will modify the data in place. 

#We can view the basis and shift vector:
basis = my_affine_vector_space.get_basis()
shift_vector = my_affine_vector_space.get_shift_vector()

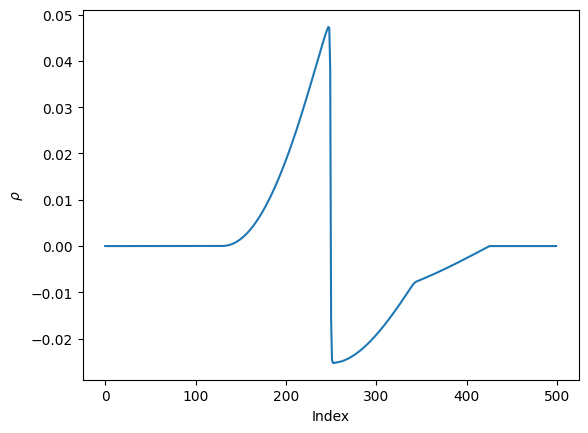
#We can look at the density compoenent of the first basis:
plt.plot(basis[0,:,0])
plt.xlabel(r'Index')
plt.ylabel(r'$\rho$')
plt.show()

[False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True]
../../_images/38ff670a8c5f8c00f4b3dc2b20827d3f1735def840b213f89635e45592d412ff.png 
# We can check the dimension of the vector space
print("The dimension of the vector space is " , my_affine_vector_space.extents())
print("The number of basis vectors in my vector space is " , my_affine_vector_space.extents()[-1])

The dimension of the vector space is  (3, 500, 30)
The number of basis vectors in my vector space is  30

# We can also check that the basis is orthonormal:
is_identity = np.einsum('ijk,ijl->kl',basis,basis)
assert(np.allclose(is_identity,np.eye(30)))

This Page