Composite vector space tutorial#

In romtools, a composite vector space refers to multiple vector spaces that are stichted together into one vector space. The use case of a composite vector space is if you want to have independent basis functions for different DOFs (e.g., mass, momentum) In this tutorial you will learn:

How to construct a composite vector space that comprises several vector spaces stiched together

#First, let's import the relavant modules:
import romtools
import numpy as np
from matplotlib import pyplot as plt
from romtools import vector_space, composite_vector_space

#Now, we will load in snapshots from a FOM. Here, we use pre-computed snapshots of the 1D Euler equations obtained using pressio-demo-apps
snapshots = np.load('snapshots.npz')['snapshots']

## The snapshots are in tensor form:
n_vars, nx, nt = snapshots.shape

# Along the first axis we have snapshots of mass (rho), momentum (rho U), and energy (rho E), respectively

## Note that romtools works with tensor forms (https://pressio.github.io/rom-tools-and-workflows/romtools/vector_space.html)

# In this example, we make a composite vector space where each state variable in our snapshot matrix has each own basis
# (This is often times referred to as "vector POD" in the literature

#Like the last tuorial, let's use a truncater that controls for how we want to truncate our basis.
my_truncater = vector_space.utils.EnergyBasedTruncater(0.999)

#Now, let's construct a vector space using POD for the DENSITY VARIABLE ONLY
my_vector_space_rho = vector_space.VectorSpaceFromPOD(snapshots[0:1],truncater=my_truncater)

#Let's look a the shape of our vector space:
print('The vector space for rho is of shape: ', my_vector_space_rho.extents())

[False False False  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True]
The vector space for rho is of shape:  (1, 500, 4)

# Now, we will make vector spaces for the next two variables (momentum and energy)
my_vector_space_rhoU = vector_space.VectorSpaceFromPOD(snapshots[1:2],truncater=my_truncater)
print('The vector space for rhoU is of shape: ', my_vector_space_rhoU.extents())
my_vector_space_rhoE = vector_space.VectorSpaceFromPOD(snapshots[2:3],truncater=my_truncater)
print('The vector space for rhoE is of shape: ', my_vector_space_rhoE.extents())

[False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True]
The vector space for rhoU is of shape:  (1, 500, 31)
[False False False False False  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True]
The vector space for rhoE is of shape:  (1, 500, 6)

# Now we will create a composite vector space that stiches these three vector spaces together:
my_composite_vector_space = composite_vector_space.CompositeVectorSpace([my_vector_space_rho,my_vector_space_rhoU,my_vector_space_rhoE])

# Let's look at the size of this vector space:
print('The composite vector space is of shape: ' , my_composite_vector_space.extents())
#We see that the number of basis vectors is the sum of the individual vector spaces

The composite vector space is of shape:  [  3 500  41]

#Let's view the sparsity pattern if we view this as a tradititional basis matrix
#First, let's grab the basis
composite_basis = my_composite_vector_space.get_basis()
#Now we will reshape it into a matrix. Note all of romtools uses order 'C' for reshaping
basis_matrix = np.reshape(composite_basis,(composite_basis.shape[0]*composite_basis.shape[1],composite_basis.shape[2]),'C')

plt.spy(basis_matrix)
plt.gca().set_aspect(0.025)
plt.show()

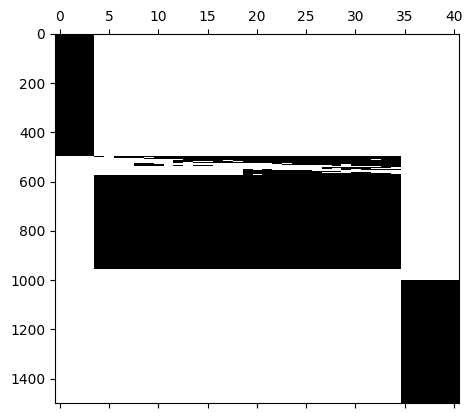
../../_images/5cc8da782c7f99613421e6b15ff235c3580e41fa80b0255635541281553aa8b0.png

# We see the basis has a block structure. This means that each state variable will effectively have their own reduced coordinates.

Composite vector space tutorial#

This Page