POD vector space tutorial

In this tutorial you will learn:

• How to construct a vector space using proper orthogonal decomposition

• How to use a truncater

#First, let's import the relavant modules:
import romtools
import numpy as np
from matplotlib import pyplot as plt
from romtools import vector_space

module 'mpi4py' is not installed

#Now, we will load in snapshots from a FOM. Here, we use pre-computed snapshots of the 1D Euler equations obtained using pressio-demo-apps
snapshots = np.load('snapshots.npz')['snapshots']

## The snapshots are in tensor form:
n_vars, nx, nt = snapshots.shape
## Note that romtools works with tensor forms (https://pressio.github.io/rom-tools-and-workflows/romtools/vector_space.html)

#Now, let's make a basis using POD that uses the first vector as an affine offset
#First, let's create a "shifter" that is responsible for shifting snapshots
#(https://pressio.github.io/rom-tools-and-workflows/romtools/vector_space/utils/shifter.html)
my_shifter = vector_space.utils.create_firstvec_shifter(snapshots)

#Now, let's create a truncater that controls for how we want to truncate our basis.
#(https://pressio.github.io/rom-tools-and-workflows/romtools/vector_space/utils/truncater.html)
#Let's use an energy-based criterion
my_truncater = vector_space.utils.EnergyBasedTruncater(0.999)

#Now, let's construct an affine vector space using POD with our shifter and truncater
#Note we don't use the first snapshot in the vector space since this is the affine offset
my_affine_vector_space = vector_space.VectorSpaceFromPOD(snapshots[...,1::],truncater=my_truncater,shifter=my_shifter)

##It's important to note that we do not do a deep copy of the snapshot matrix for performance reasons.
##Once you pass us the snapshot tensor, we will modify the data in place. 

#We can view the basis and shift vector:
basis = my_affine_vector_space.get_basis()
shift_vector = my_affine_vector_space.get_shift_vector()

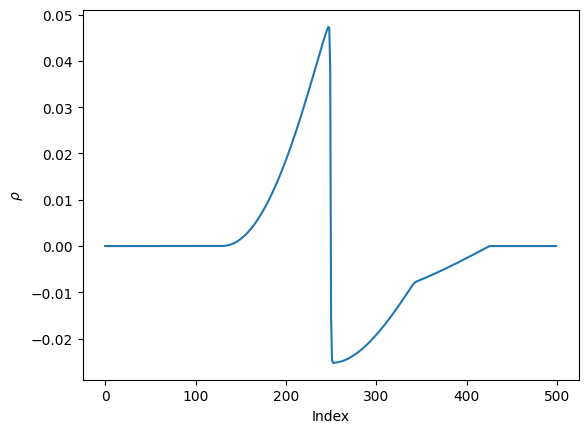
#We can look at the density compoenent of the first basis:
plt.plot(basis[0,:,0])
plt.xlabel(r'Index')
plt.ylabel(r'$\rho$')
plt.show()

# We can check the dimension of the vector space
print("The dimension of the vector space is " , my_affine_vector_space.extents())
print("The number of basis vectors in my vector space is " , my_affine_vector_space.extents()[-1])

The dimension of the vector space is  (3, 500, 30)
The number of basis vectors in my vector space is  30

# We can also check that the basis is orthonormal:
is_identity = np.einsum('ijk,ijl->kl',basis,basis)
assert(np.allclose(is_identity,np.eye(30)))