example 1

#include "pressio/ode_advancers.hpp"
#include "pressio/ode_steppers_explicit.hpp"
#include <Eigen/Core>

template<class ScalarType>
class SimpleSystem{
public:
  using independent_variable_type = ScalarType;
  using state_type                = Eigen::Matrix<ScalarType,-1,1>;
  using rhs_type	          = state_type;

  state_type createState() const{
    auto s = state_type(3);
    s.setConstant(0);
    return s;
  };

  rhs_type createRhs() const{
    auto v = rhs_type(3);
    v.setConstant(0);
    return v;
  };

  void rhs(const state_type & state,
	   const independent_variable_type timeIn,
	   rhs_type & rhs) const
  {
    constexpr ScalarType ten{10};
    rhs(0) = ten * state(0);
    rhs(1) = ten * state(1);
    rhs(2) = ten * state(2);
  };
};

int main(int argc, char *argv[])
{
  PRESSIOLOG_INITIALIZE(pressiolog::LogLevel::sparse);

  using scalar_type = double;
  SimpleSystem<scalar_type> problem;

  auto y = problem.createState();

  namespace pode = pressio::ode;
  constexpr auto scheme = pode::StepScheme::ForwardEuler;
  auto stepperObj = pode::create_explicit_stepper(scheme, problem);

  {
    /*
      run a fixed number of steps
    */
    y(0) = 1.; y(1) = 2.; y(2) = 3.;
    const scalar_type dt{0.1};
    const scalar_type startTime{0.0};
    pode::advance_n_steps(stepperObj, y, startTime, dt, pode::StepCount{1});
    // check solution
    std::cout << "Computed solution: ["
	      << y(0) << " " << y(1) << " " << y(2) << "] "
	      << "Expected solution: [2,4,6] \n";
  }
  std::cout << std::endl;

  {
    /*
      run until target time
    */
    y(0) = 1.; y(1) = 2.; y(2) = 3.;
    const scalar_type startTime{0.0};
    const scalar_type finalTime{1.0};
    pode::advance_to_target_point(stepperObj, y, startTime, finalTime,
				  [](const pode::StepCount & /*unused*/,
				     const pode::StepStartAt<scalar_type> & /*unused*/,
				     pode::StepSize<scalar_type> & dt)
				  {
				    dt = 0.1;
				  });
    // check solution
    std::cout << "Computed solution: ["
	      << y(0) << " " << y(1) << " " << y(2) << "] "
	      << "Expected solution: [1024, 2048, 3074] \n";
  }

  std::cout << "PASSED\n";
  PRESSIOLOG_FINALIZE();
  return 0;
}

example 2

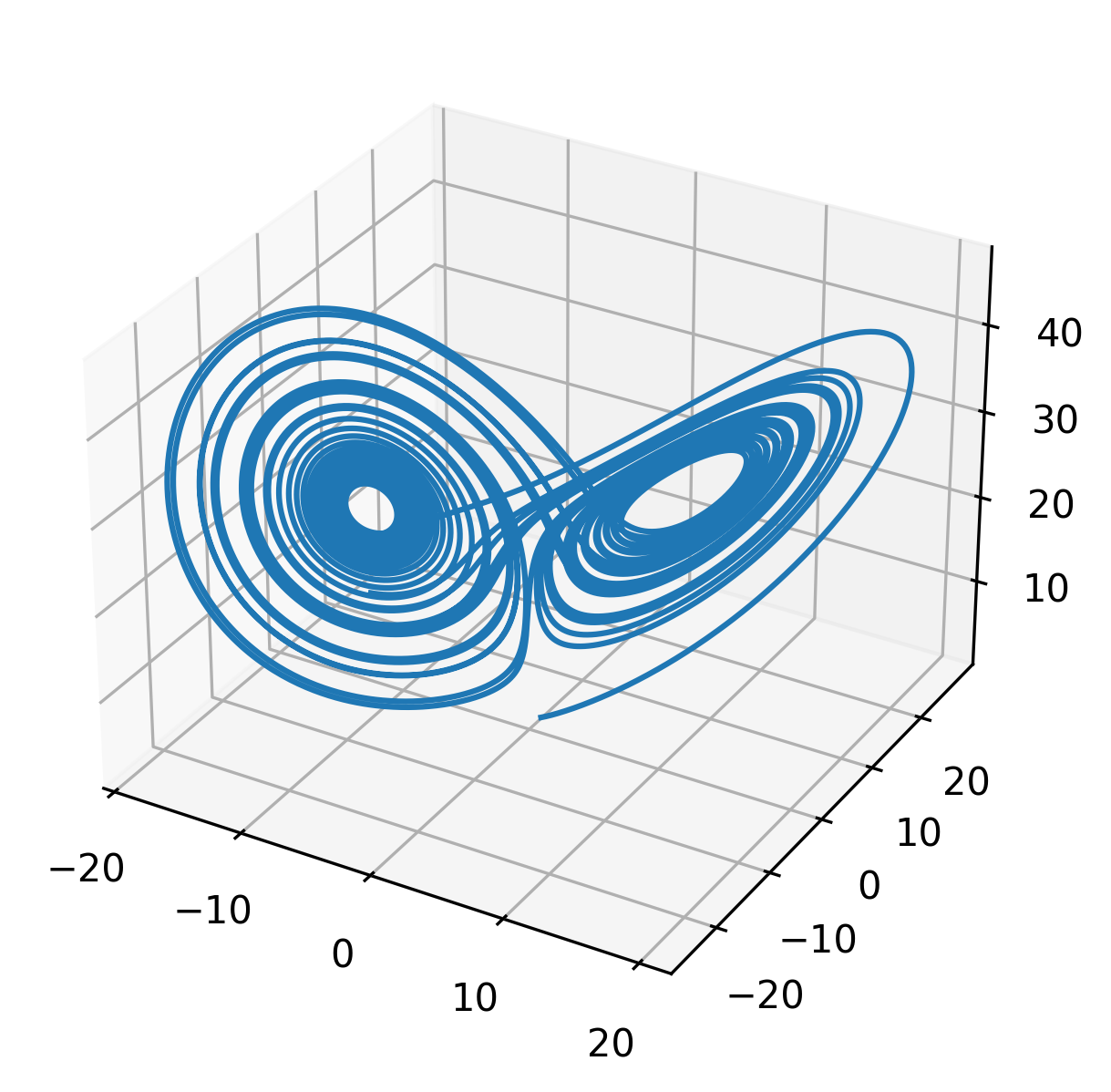
Integrate the original Lorenz system via explicit time integration.

#include "pressio/ode_advancers.hpp"
#include "pressio/ode_steppers_explicit.hpp"
#include <Eigen/Core>

template<class ScalarType>
class Lorenz3{
  const int N_ = 3;
  const ScalarType rho_   = static_cast<ScalarType>(28);
  const ScalarType sigma_ = static_cast<ScalarType>(10);
  const ScalarType beta_  = static_cast<ScalarType>(8)/3;

public:
  using independent_variable_type = ScalarType;
  using state_type                = Eigen::Matrix<ScalarType,-1,1>;
  using rhs_type      = state_type;

  state_type createState() const{
    auto s = state_type(N_);
    s.setConstant(0);
    return s;
  };

  rhs_type createRhs() const{
    auto v = rhs_type(N_);
    v.setConstant(0);
    return v;
  };

  void rhs(const state_type & state,
	   const independent_variable_type timeIn,
	   rhs_type & rhs) const
  {
    const auto x = state(0);
    const auto y = state(1);
    const auto z = state(2);

    rhs(0) = sigma_ * (y - x);
    rhs(1) = x * (rho_ - z) - y;
    rhs(2) = x * y - beta_ * z;
  };
};

template<class ScalarType>
class StateObserver
{
public:
  explicit StateObserver(int sampleFreq)
    : myfile_("state_snapshots.bin",  std::ios::out | std::ios::binary),
      sampleFreq_(sampleFreq){}

  ~StateObserver(){ myfile_.close(); }

  template<typename TimeType>
  void operator()(pressio::ode::StepCount step,
		  const TimeType /*timeIn*/,
		  const Eigen::Matrix<ScalarType,-1,1> & state)
  {
    if (step.get() % sampleFreq_ == 0){
      const std::size_t ext = state.size()*sizeof(ScalarType);
      myfile_.write(reinterpret_cast<const char*>(&state(0)), ext);
    }
  }

private:
  std::ofstream myfile_;
  const int sampleFreq_ = {};
};

int main(int argc, char *argv[])
{
  PRESSIOLOG_INITIALIZE(pressiolog::LogLevel::sparse);

  using scalar_type = double;
  Lorenz3<scalar_type> problem;

  namespace pode = pressio::ode;
  constexpr auto scheme = pode::StepScheme::RungeKutta4;
  auto stepperObj = pode::create_explicit_stepper(scheme, problem);

  auto y = problem.createState();
  y(0) = 0.5; y(1) = 1.0; y(2) = 1.;
  const scalar_type startTime{0.0};
  const scalar_type finalTime{40.0};
  const int stateSampleFreq = 2;
  pode::advance_to_target_point(stepperObj, y, startTime,
				finalTime,
				  [=](const pode::StepCount & /*unused*/,
				     const pode::StepStartAt<scalar_type> & /*unused*/,
				     pode::StepSize<scalar_type> & dt)
				  { dt = 0.01; },
				StateObserver<scalar_type>{stateSampleFreq});

  std::cout << "PASSED\n";
  PRESSIOLOG_FINALIZE();
  return 0;
}

Visualize

You can use the data collected to plot the results via the following script:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

if __name__== "__main__":
    numVars = 3
    D = np.fromfile("./state_snapshots.bin")
    numTimeSteps = int(np.size(D)/numVars)
    print(numTimeSteps)
    #D  = np.reshape(data, (numTimeSteps, numVars))

    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1, projection='3d')
    ax.plot(D[0::3], D[1::3], D[2::3])
    fig.savefig("plot.png", format="png", bbox_inches='tight', dpi=300)
    plt.show()

example 3

Integrate the original Lorenz system using implicit time integration.

#include "pressio/ode_advancers.hpp"
#include "pressio/ode_steppers_implicit.hpp"
#include <Eigen/Core>

template<class ScalarType>
class Lorenz3{
  const int N_ = 3;
  const ScalarType rho_   = static_cast<ScalarType>(28);
  const ScalarType sigma_ = static_cast<ScalarType>(10);
  const ScalarType beta_  = static_cast<ScalarType>(8)/3;

  using trip_t = Eigen::Triplet<ScalarType>;
  mutable std::vector<trip_t> tripletList_;

public:
  using independent_variable_type = ScalarType;
  using state_type                = Eigen::Matrix<ScalarType,-1,1>;
  using rhs_type		  = state_type;
  // since the Jacobain of Lorenz3 is fairly dens,
  // we could use a dense matrix for it, but we use a sparse one
  // here for demonstration purposes
  using jacobian_type             = Eigen::SparseMatrix<ScalarType>;

  Lorenz3(){
    allocateTriplets();
  }

  state_type createState() const{
    state_type s(N_);
    s.setConstant(0);
    return s;
  };

  rhs_type createRhs() const{
    rhs_type v(N_);
    v.setConstant(0);
    return v;
  };

  jacobian_type createJacobian() const{
    jacobian_type J(N_, N_);
    J.setFromTriplets(tripletList_.begin(), tripletList_.end());
    return J;
  };

  void rhsAndJacobian(const state_type & state,
		      const independent_variable_type timeIn,
		      rhs_type & rhs,
		      std::optional<jacobian_type*> Jopt) const
  {
    const auto x = state(0);
    const auto y = state(1);
    const auto z = state(2);

    rhs(0) = sigma_ * (y - x);
    rhs(1) = x * (rho_ - z) - y;
    rhs(2) = x * y - beta_ * z;

    if (Jopt)
    {
      auto & J = *Jopt.value();
      tripletList_[0] = {0, 0, -sigma_};
      tripletList_[1] = {0, 1,  sigma_};

      tripletList_[2] = {1, 0, rho_-z};
      tripletList_[3] = {1, 1, -1.};
      tripletList_[4] = {1, 2, -x};

      tripletList_[5] = {2, 0, y};
      tripletList_[6] = {2, 1, x};
      tripletList_[7] = {2, 2, -beta_};
      J.setFromTriplets(tripletList_.begin(), tripletList_.end());
    }
  };

private:
  void allocateTriplets()
  {
    // first row
    tripletList_.push_back( trip_t( 0, 0, 0.) );
    tripletList_.push_back( trip_t( 0, 1, 0.) );
    // second and third row
    for (int i=1; i<=2; ++i){
      tripletList_.push_back( trip_t( i, 0, 0.) );
      tripletList_.push_back( trip_t( i, 1, 0.) );
      tripletList_.push_back( trip_t( i, 2, 0.) );
    }
  }
};

int main(int argc, char *argv[])
{
  PRESSIOLOG_INITIALIZE(pressiolog::LogLevel::sparse);

  using scalar_type = double;
  using problem_type = Lorenz3<scalar_type>;
  problem_type problem;

  namespace pode = pressio::ode;
  namespace plins  = pressio::linearsolvers;

  // create stepper
  constexpr auto scheme = pode::StepScheme::BDF2;
  auto stepper = pode::create_implicit_stepper(scheme, problem);

  // linear and nonlinear solver
  using fom_jacobian_t = typename problem_type::jacobian_type;
  using linear_solver_t = plins::Solver<plins::iterative::Bicgstab, fom_jacobian_t>;
  linear_solver_t linearSolver;

  auto nonLinearSolver = pressio::create_newton_solver(stepper, linearSolver);
  nonLinearSolver.setStopTolerance(1e-13);

  auto y = problem.createState();
  y(0) = 0.5; y(1) = 1.0; y(2) = 1.;
  const scalar_type startTime{0.0};
  const scalar_type finalTime{40.0};
  std::ofstream myfile("state_snapshots.bin",  std::ios::out | std::ios::binary);
  pode::advance_to_target_point(stepper, y, startTime, finalTime,
				// lambda to set the time step
				[](const pode::StepCount & /*unused*/,
				   const pode::StepStartAt<scalar_type> & /*unused*/,
				   pode::StepSize<scalar_type> & dt)
				{ dt = 0.01; },
				// lambda to observe and write to file the state
				[&](pressio::ode::StepCount step,
				    const scalar_type /*timeIn*/,
				    const typename problem_type::state_type & state)
				{
				  std::cout << "saving state at = " << step.get() << "\n";
				  const std::size_t ext = state.size()*sizeof(scalar_type);
				  myfile.write(reinterpret_cast<const char*>(&state(0)), ext);
				},
				nonLinearSolver);
  myfile.close();

  std::cout << "PASSED\n";
  PRESSIOLOG_FINALIZE();
  return 0;
}

Visualize

You can visualize the results using the same Python script above.